Paikanmääritys tähdistä Marcq Saint Hilairen ”intercept” metodilla

Katso alla olevaa kuvaa. Siinä on kaksi tähteä, joiden korkeudet voit mitata ja siten saat selville etäisyytesi tähden projektiopisteeseen. Sinulla on tarkka kello, kronometri, joka näyttää Greenwichin aikaa. Nautical Almanacista saat selville näiden kahden tähden deklinaation (dec) ja sideerisen tuntikulman (SHA). Samoin saat selville Arieksen Greenwichin tuntikulman ( GHA). Tästä voit laskea kummankin tähden Greenwichin tuntikulman (GHA). Kun tiedät tähtien deklinaation ja Greenwichin tuntikulman, voit löytää niiden projektiopisteen maapallolla. Korkeusmittauksesta sait selville sijoittajaympyrän säteen, joka on 90° - tähden korkeus horisontista. Sijoittajaympyrän säde asteina kerrottuna 60:llä on sen säde meripeninkulmissa.

Nyt sinun vain pitää piirtää kartalle kaksi isoa sijoistusympyrää, joiden keskipisteet ovat tähtien projektiopisteitä.

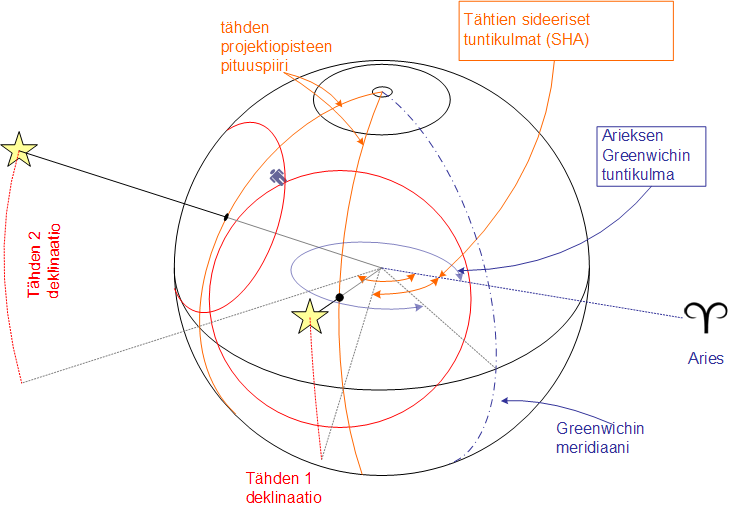
Tässä on ongelma. Merikortit yleensä kattavat vain pienen pienen osan maapallosta. Käytännössä yllä kuvattu menetelmä ei siis toimi. Pitää vähän säätää.

Pitää jotenkin järjestää että tarvitsee piirtää vain osa Sijoittajaympyrästä. Ratkaisu on tämä. Piirretään vain osa sijoittajaympyröistä. Se osa, joka osuu kartallesi.

Kuten kuvasta yllä näkyy, ympyrät ovat isoja. Jos tähti on vain 10° kulmassa zeniitistäsi, on projektiopisteeseen matkaa 60 meripeninkulmaa. Sellainen tähti on lähes pääsi päällä ja sen korkeutta horisontista on lähes mahdoton mitata. Jos tähti on 50° korkeudella horisontista on sinun ja sen projektiopisteen välinen matka (90°-50°)*60 = 2400 meripeninkulmaa. Jos merikorttisi reuna on vaikka niinkin iso kuin 100 meripeninkulmaa, on sille osuva sijoittajaympyrän palanen käytännössä suora viiva. Sen kaarevuus tällä etäisyydellä tähden projektiopisteestä on huomaamaton.

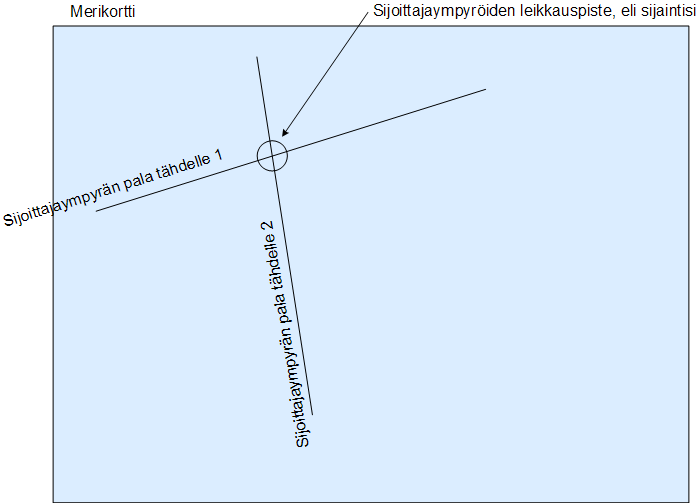Siispä piirretään kaksi viivaa, jotka ovat yllä olevien tähtien asemaympyröiden osia.

Hyvä idea, eikös.

Jaa mutta mitenkä ympyrän kehän palasen osaa piirtää oikeaan kohtaan? Jos me löydämme edes yhden pisteen sijoittajaympyrältä, me voimme piirtää sijoittajaympyrän palasen sen pisteen kautta.

Marcq Saint Hilaire ratkaisi asian tällä tavalla:

  1. Valitaan jokin piste P, joka on alle 60 meripeninkulman päässä meidän todellisesta paikastamme. Sen tarkempi ei tarvitse olla.
  2. Lasketaan missä suunnassa tähden projektiopiste on pisteestä P. Tämä tarkoittaa nauttisen kolmion ratkaisemista olettaen että että valittu piste P on sijaintisi. Siksi pistettä P usein kutsutaan oletetuksi paikaksi tai englanniksi assumed position (AP). Laskun ratkaisuun tarvitset paikallisen tuntikulman (LHA) tähden projektiopisteeseen ja tähden deklinaation (dec). Niiden avulla saat Sight Reduction Tables kirjasesta selville atsimuutin ja tähden korkeuden horisontista valitusta pisteestä katsottuna. Atsimuutin avulla voit laskea tosisuuntiman kohti tähden projektiopistettä. Katso kappale Tosisuuntima tähteen.
  3. Piirretään tästä valitusta pisteestä P viiva kohti tähden projektiopistettä. Viivan suunta laskettiin kohdassa 2, tosisuuntima kohti tähden projektiopistettä.
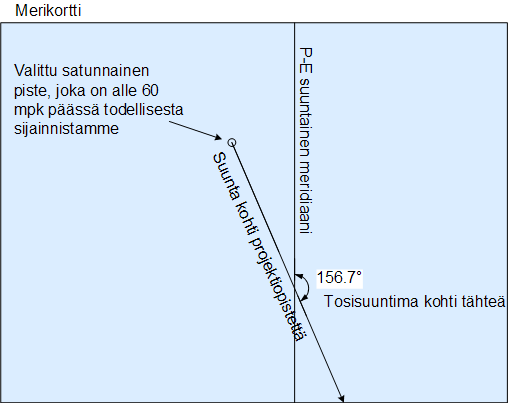
  4. Kohdassa 2 saimme selville myös tähden korkeuden valitussa pisteessä P. Sen lisäksi me mittaismme itse tähden korkeuden sekstantilla. Nyt voimme laskea kuinka paljon lähempänä tai kauempana olemme tähden projektiopisteestä kuin valittu piste P. Etäisyyden ero on yhtä suuri kuin tähden mitatun korkeuden ja korkeuden paikassa P erotus muutettuna merimaileksi. Katso kappale Kulmien, asteiden ja meripeninkulman suhde toisiinsa maapallon pinnalla sivulla 29. Jos mitattu korkeus on suurempi kuin laskettu korkeus pisteessä P, on todellinen sijainti lähempänä projektiopistettä kuin piste P. Jos korkeus on pienempi, on todellinen sijainti kauempana.
  5. Merkitään pisteen P ja sijaintimme etäisyysero projektiopisteestä kartalle pitkin pisteen P kautta kulkevaa suuntimaviivaa.

    Esimerkissä mitattu korkeus oli pienempi, joten olemme kauempana projektiopisteestä kuin valittu piste P.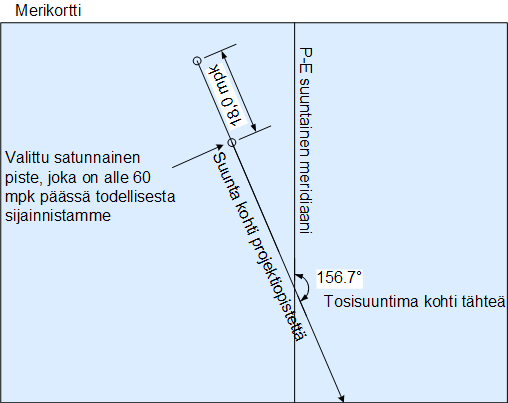
  6. Näin saimme selville yhden pisteen sijoittajaympyrällä sekä suunnan kohti projektiopistettä. Sijoittajaympyrä on suorassa kulmassa suuntaan kohti projektiopistettä, joten osaamme piirtää sijoittajaympyrän palan merikortille.

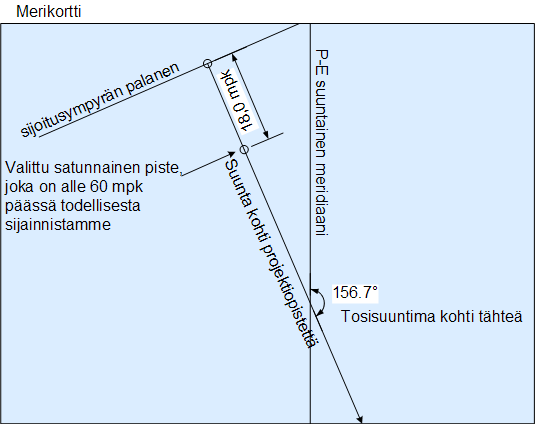
Jos olisimme valinneet alussa jonkin toisen pisteen P2, olisi lopputulos silti sama. Tähden laskettu korkeus eri pisteestä olisi eri ja sen ja mitatun korkeuden ero sellainen, että sijoittajaympyrä olisi edelleen tullut samaan kohtaan. Alla olevassa esimerkissä P2 pisteelle laskettu korkeus tähteen on pienempi kuin mitattu korkeus. Siksi tiedämme että olemme lähempänä tähden projektiopistettä kuin kohta P2 ja osaamme piirtää suuntimaa kohtisuorassa olevan sijoittajaympyrän palasen korkeuseron verran lähemmäksi projektiopistettä. Sijoittajaympyrä päättyy näin täsmälleen samaan kohtaan riippumatta siitä minkä satunnaisen pisteen valitsemme.

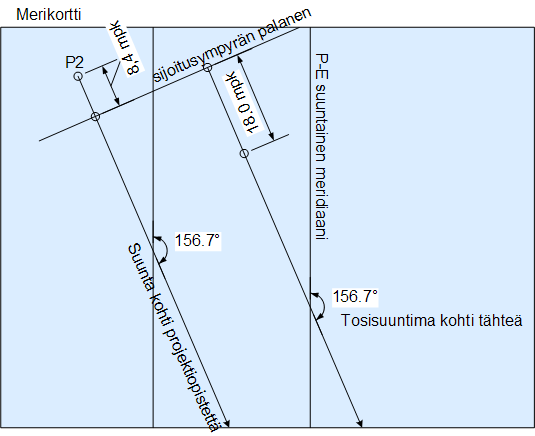
Kun piirrämme samalle kartalle suunnan toiseen tähteen ja sen sijoittajaympyrän palasen, saamme selville sijaintimme. Sitä varten voimme valita minkä tahansa sopivan kolmannen pisteen, P3.

Siinä se. Näin se toimii.

s i s ä l l y s

Hamburg VII 2013