Nauttisen kolmion ratkaiseminen eli korkeuslasku

Ratkaisun voi hakea joko laskimella tai sitten siihen tarkoitukseen tehdyillä taulukoilla. Ennen laskukoneita käytettiin ihmisiä etukäteen laskemaan monimutkaisia laskutoimituksia ja nämä ratkaisut löytyivät erilaisista taulukkokirjoista. Tähtimerenkulussa käytetään vielä taulukkokirjaa sen luotettavuuden takia. Kirja toimii vaikka patterit olisivat laskimesta loppu.

Esimerkiksi NP 401 Sight Reduction tables for marine navigation auttaa ratkaisemaan nauttisen kolmion. Talukosta voit lukea tähden korkeuden horisontista ja atsimuutin. Lähtötietoina tarvitset oletetun paikan leveyspiirin (latitudin) ja pituuspiirin (longitudin), tähden paikallisen tuntikulman (LHA) sekä tähden deklinaation. Tähden deklinaation ja sideerisen tuntikulman saat Nautical Almanac kirjasta. Sideerisestä tuntikulmasta taas voi laskea paikallisen tuntikulman pituuspiirin (longitudi, lon) avulla. Katso kappale Paikallinen tuntikulma (LHA).

Tyypillisesti riittää että meillä on tiedossa arvioitu tämänhetkinen pituuspiiri. Oletetun paikan saat purjehtiessasi tekemistäsi merkintälaskuista. Paikan määrityksessä olettu paikka saa heittää todellisesta 60 meripeninkulmaa ja silti tulos on vielä riittävän tarkka. Jos käytät taulukkoa toiseen suuntaan eli pyrit tunnistamaan tähteä (tästä myöhemmin) saat tuloksen kuitenkin riittävällä tarkkuudella, jotta erotat navigointiin tarkoitettavat tähdet, planeetat, kuun ja auringon toisistaan. Auringon tunnistamiseen on kyllä helmpompiakin keinoja.

Kirjan Sight Reduction Tables aukeamat on järjestetty paikallisen tuntikulman (LHA) mukaan. Aukeamalla on neljän eri tuntikulman perusteella lasketut tulokset. Kuvassa ne ovat LHA1, LHA2, LHA3 ja LHA4. Kuten kuvasta näkyy, kun LHA1 on pienempi kuin 90° ja LHA2 = 360° - LHA1, ovat muodostuneet nauttiset kolmiot toistensa peilikuvia. Kulman ja sivujen pituudet ovat yhtäsuuret. Tilan säästämiseksi lukuja ei tarvitse kertoa kahteen kertaan. Pitää vain tietää onko atsimuutti itäistä vain läntistä.

NP 401 Sight Reduction tables for marine navigation kirjan aukeaman vasen sivu ja oikean sivun alapuoli ovat ns. SAME aluetta. Kun tähden deklinaatio on pohjoista, eli sen projektiopiste on päiväntasaajan pohjoispuolella, ja sinä olet itse pohjoisella pallonpuoliskolla, katsotaan nauttisen kolmion ratkaisu SAME alueelta.

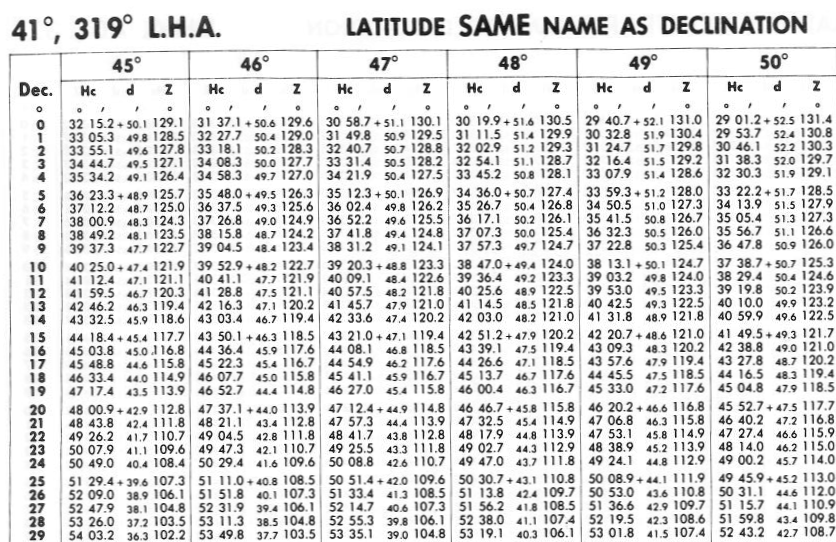
Kuvassa Sight Reduction Table aukeaman vasemmanpuoleisen sivun osa. Siinä on niiden tähtien projektiopisteiden korkeus (Hc) ja atsimuutti (Z), joiden paikallinen tuntikulma (LHA) on 41° tai 319° = 360 - 41°. Kuten edellisestä kuvasta näkyy, nämä ovat samanlaisia kolmioita paitsi että ne ovat toistensa peilikuvia. Jos kääntäisit Sight Reduction Tablein sivua, seuraava aukeama listaisi ratkaisut nauttiselle kolmiolle, jossa paikallinen tuntikulma (LHA) on 42°.

Sarakkeet 45°, 46°, 47°, jne ovat leveyspiirejä (eng. latitude) ja antavat ratkaisujen arvot riippuen sijainnistasi. Yhteen kirjaan ei mahdu kaikki leveyspiirit. Itämerellä käytettäväksi sopii Sight Reduction Tables for Marine Navigation Latitudes 45° - 60°. Samaa kirjaa voi käyttää kaikilla leveyspiireillä 45° - 60° pohjoista tai eteläistä leveyttä. Edelliset ratkaisut toimivat myös eteläisellä pallonpuoliskolla kunhan vain muutat pohjoisen taivaan navan eteläiseksi ja ajattelet atsimuutin olevan etelästä länteen tai itään. Tosisuuntimaa laskiessa pitää vain muistaa onko päiväntasaajan pohjois- vai eteläpuolella. Katso kappaletta Tosisuuntima tähteen.

Oikean sivun yläreunassa on CONTRARY alue.

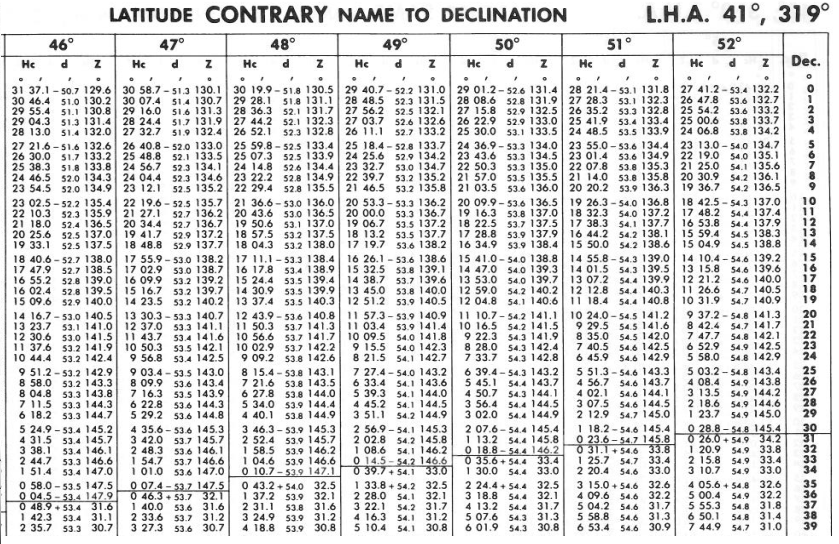
Tämän alueen tähtien projektiopiste on eri pallonpuoliskolla kuin sinä. Oikeanpuoleisen sivun reunassa ovat deklinaatiot alkaen nollasta ylöspäin. Ne ovat siis eteläisen pallonpuoliskon deklinaatioita, jos sinä olet pohjoisella pallonpuoliskolla. Jos olet esimerkiksi leveysasteella 45° pohjoista, tähti on sinusta suoraan etelässä eli sen paikallinen tuntikulma on 0° ja tähden deklinaatio on 45° eteläistä, sen korkeus on silloin parhaimmillaankin 0°. Se on horisontissasi. Kun maapallo pyörii ja tähden paikallinen tuntikulma kasvaa, se vaipuu heti horisontin alle.

Alla koko Sight Reduction Tablein oikeanpuoleinen sivu, jolla paikallinen tuntikulma (LHA) on 41°. Jos kääntäisit Sight Reduction Tablein sivua, seuraava aukeama listaisi ratkaisut nauttiselle kolmiolle, jossa paikallinen tuntikulma (LHA) on 42°.

Tästä näet että jos olet esimerkiksi latitudilla 45°, pystyt näkemään tähden, joka on sinusta tosisuunnassa (tosisuunta = atsimuutti) 148,4° tai 360° - atsimuutti = 360° - 148,4° = 211,6°, ja jonka projektiopiste on eteläisellä leveyspiirillä S 37°. Näet sen juuri ja juuri horisontin yläpuolella. Sight Reduction Tableista näet että se on 2,2° horisontin yläpuolella.

Tähti, joka on samassa suunnassa ja jonka projektiopiste on sitä etelämmässä, on horisonttisi alla. Tässä välissä sarakkeessa 45° on viiva. Sen sijaan tähti jonka deklinaatio on pohjoisella leveyspiirillä N 38° on näkyvissä sinusta pohjoiseen. Sen paikallinen tuntikulma (LHA) on 180° - 41° = 139° tai 180° + 41° = 221°, kuten näet sivun oikeasta alareunasta. Kappaleen ensimmäisessä kuvassa nämä ovat tähtiä, joiden paikallinen tuntikulma on LHA3 tai LHA4. Ne näkyisivät sinusta joko tosisuunnassa 31,1° tai 360° – atsimuutti = 360° - 31,1° = 328,9°.

Jos olet astetta pohjoisempana, 46° leveyspiirillä, et enää näe tähteä jonka projektiopiste on eteläisellä leveyspiirillä S 37°. Se on laskenut horisontin alle kun siirryit pohjoiseen. Sen sijaan pohjoisesta on noussut horisontin alta näkyviin tähti, jonka paikallinen tuntikulma (LHA) on 139° tai 221°, ja jonka projektiopiste on pohjoisella leveyspiirillä N 37°.

Ellet mennyt edellisestä täysin sekaisin, saatoit huomata että taulukkokirjan aukeamalla on ratkaisut vain sellaisille nauttisille kolmioille, joissa paikallinen tuntikulma (LHA) on kokonaisia asteita. Näin on. Muita tuntikulmia ei tarvita myöhemmin selviävistä syistä. Me tarvitsemme kuitenkin ratkaisuja sellaisille nauttisille kolmioille, joissa taivaankappaleen deklinaatio (dec) on jotain muuta kuin täysiä asteita. Näissä tapauksissa käytetään interpolointia. Kirjasta löytyy interpolointitaulukko, jonka avulla pystyt laskemaan tähden korkeuden horisontista, vaikka sen deklinaatio ei olisi täysiä asteita.

Interpolointi tarkoittaa että johdetaan taulukon kahden luvun väliin osuva arvo edellisestä ja seuraavasta arvosta.

s i s ä l l y s

Hamburg VII 2013